Сложение матриц онлайн

Сложение матриц

Сложение матриц А и В – это нахождение такой матрицы С, все элементы которой представляют собой сложенные попарно соответствующие элементы исходных матриц А и В. Складывать допускается только матрицы одинаковой размерности (допустим m × n), т.е. имеющие равное количество строк и равное количество столбцов.

Таким образом, математически сумма матриц выглядит так:

Аm×n + Bm×n = Cm×n

Каждый элемент искомой матрицы равен сумме соответствующих элементов заданных матриц:

cij = aij + bij,

где i принимает значение от 1 до m, j имеет значения от 1 до n.

Рассмотрим пример сложения двух матриц размера 2 × 3.
Даны две матрицы:

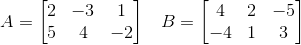
Найти сумму матриц А и В.
Решение:

Свойства сложения матриц:

1. Коммутативность – переместительный математический закон, согласно которому результат сложения матриц не зависит от их перестановки.
   A + В = В + А
2. Ассоциативность – сочетательный математический закон, согласно которому результат сложения матриц не зависит от последовательности расстановки скобок.
   А + (В + С) = (А + В) + С
3. Сложение с нулевой матрицей – для любой матрицы существует нейтральный элемент, которым является нулевая матрица, сложение с которым не изменяет исходную матрицу.
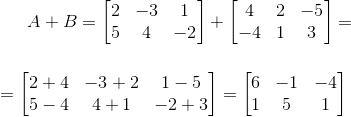
   Нулевая матрица O – матрица, все элементы которой имеют нулевое значение.
   А + О = А
4. Существование противоположной матрицы – для ненулевой матрицы А всегда существует матрица –А, суммой которых является нулевая матрица.
   А + (-А) = О

Решение