Найти определитель матрицы онлайн

Определитель (детерминант) матрицы

Понятие "определитель" применимо только к квадратным матрицам.
Квадратная матрица размером 2 х 2 также называется матрицей 2-го порядка.
А в общем случаем квадратная матрица размером n x n называется матрицей n-го порядка.
В соответствии с этим есть определители 2-го порядка, определители 3-го порядка, определители 4-го порядка и так далее.

Допустим дана квадратная матрица A, тогда определитель матрицы A обозначается |A|, либо det(A), либо ΔA.

Определитель 1-го порядка

Определитель матрицы первого порядка (когда матрица состоит всего из одного элемента a11) равен её единственному элементу: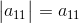

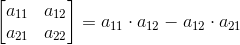
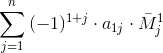
Определитель 2-го порядка

Чтобы вычислить определитель матрицы второго порядка нужно взять произведение элементов главной диагонали матрицы (диагонали, идущий из верхнего левого угла в нижний правый) и вычесть из него произвдение элементов, расположенных на второй диагонали.

Определитель 3-го, 4-го и более высоких порядков

Для вычисления определителя матрицы 3-го и более высокого порядка применяется формула:

где
j - номер столбца матрицы,
Mj1 - определитель матрицы, получившейся из исходной вычеркиванием 1-ой строки и j-го столбца.

Решение