
Транспонирование матрицы онлайн
|

|
Пусть имеется прямоугольная матрица А размером m x n.
Если поменять строки этой матрицы на столбцы, то получится новая матрица размером n x m, которая называется
транспонированной по отношению к А и обозначается АT.
Операция транспонирования матрицы обозначается буквой T в правом верхнем углу над матрицей. Например:
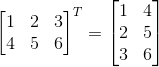
Транспонированная матрица обладает рядом свойств:
A квадратная, то её определитель равен определителю транспонированной матрицы det A = det АTA транспонировать дважды, получится сама исходная матрица: (АT)T = A(А + B)T = АT + BT(А · B)T = BT · АT(с · А)T = с · (A)T
в качестве элементов матрицы вводить целые и дробные числа, а также выражения с переменной x
(например, в ячейку матрицы можно ввести 2x, или sin(x), или даже ((x+2)^2)/lg(x)).
Полный список доступных функций можно найти в справке.