
Умножение матрицы на число онлайн
|

|
Операция умножения матрицы А на число k заключается в построении матрицы
kA = [kaij]. Умножение матрицы на число допустимо для матриц любого размера,
результатом умножения является матрица того же порядка, что и исходная матрица.
Таким образом, произведение матрицы А на число k – это результирующая матрица
B = kA того же порядка, полученная умножением всех элементов aij
исходной матрицы на заданное число.
Математически умножение матрицы на число можно представить следующими выражениями:
Аm×n × k = Вm×n
aij × k = bij,
где i принимает значение от 1 до m,
j имеет значения от 1 до n
Даны матрица А и число k:
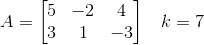
Найти произведение матрицы и числа.
Решение:
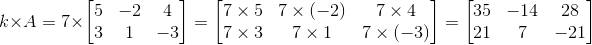
1×А = А
0×А = О
k×(А+B) = k×A + k×B
(k+n)×А = k×A + n×A
(k×n)×А = k×(n×A)
в качестве элементов матрицы вводить целые и дробные числа, а также выражения с переменной x
(например, в ячейку матрицы можно ввести 2x, или sin(x), или даже ((x+2)^2)/lg(x)).
Полный список доступных функций можно найти в справке.